
自出身之刻,咱们在成长的摇篮中便启动与数学的再会,其历史以至早于讲话的习得。当宝宝们牙牙学语成濑心美作品,父母亲便启动发蒙咱们相识数字,继而引颈咱们干预加减的数学寰球。干预学龄期,数学成为与语文相似迫切的学科,精细相伴咱们的学习岁月。

对陈腐的民族而言,数学是一个令东谈主千里醉的辩论鸿沟,他们关于整数的调和与对称有着树大根深的信念,合计整数无疑是寰宇万物的精准刻画。
然则,一次不经意的发现透顶推翻了古东谈主对数学的并吞。当东谈主们辩论等腰直角三角形,并发现斜边长为根号2时,他们试图探求根号2的实在性质,从此开启了对“根号2”的无穷探寻。

根号2的出现,宣告了格外数的建立,也冲破了东谈主们关于整数所构建的调和寰宇的幻想。格外数的发现迫使东谈主们吊销对整数的固有追求,转而投身于格外数的辩论,同期也为东谈主类带来了对无限宗旨的初次想考。
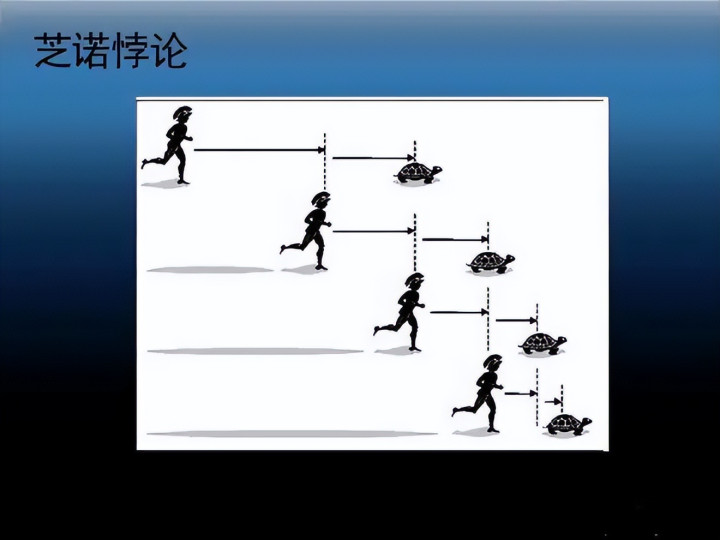
一个经典的想考就是“芝诺悖论”:设计你与一只乌龟进行竞走,你的速率为乌龟的十倍,而乌龟在你前列一百米处启动。当你追完一百米时,乌龟又前进了十米,如斯无穷尽也。字据这么的逻辑,你似乎永远也追不上乌龟。
 成濑心美作品
成濑心美作品
然则,在实验中你无疑会马上跳动乌龟。这就需要咱们真切想考无穷的宗旨,并最终并吞,天然路程不错无限细分,需要无穷多的时分来完成,但你却领有有限的时分,无法完成无穷多的事情。借助极限的宗旨,这么的悖论便应刃而解。
格外数与无穷宗旨的探索引颈东谈主类走出了第一次数学危险。又过了两千年,第二次数学危险随微积分想想的出现而起。
在牛顿的时期,东谈主们尚未透顶并吞0与无穷之间的关系,关于积分、微分和导数的信得过含义也一知半解。举例,在求解弧线上某点的切线斜率时,当代的法子是在该点隔邻取一个边长无限小的直角三角形,用三角形的斜边代替切线的斜率。

但东谈主们内心长久存有一个猜忌:不管直角三角形何等小,其斜边终究无法与切线斜率全齐等同。两者之间似乎总存在狭窄的差距。
这种无限贴近的宗旨,雷同于0.999999...与1是否尽头的问题,组成了数学史上的第二次危险,根源在于对微积分的并吞偏差。
继而,在第二次危险之后的两百多年,第三次数学危险围绕采集论的盘考而起,其中最为著明的就是“罗素悖论”。

以一个剃头师为例,他宣称只为那些不当作我方剃头的东谈主持事,那么问题来了:这位剃头师是否不错为我方剃头?若能,则抵御了他的告白;若不行,相似存在问题,因为他宣称我方能为不行自剃头的东谈主持事。
罗素悖论像是对采集论界说的辩白,即使咱们相识到这是辩白,也难以明确评释其背后的矛盾地方。这就像“天主能否创造出他我方搬不动的石头”这么的问题一样,不管陈述能或不行,齐会堕入逻辑矛盾。

从形而上学角度看,罗素悖论实则反应了唯心目的与唯物目的之间的争辩。若你握唯心目的不雅点,会合计寰球仅仅你刚烈的家具,那么“你”自己是否亦然刚烈的虚拟?“你”对“自我宗旨”的质疑是否亦然虚无的?这种质疑的质疑又若何呢?最终,咱们濒临一个根柢问题:“你”的存在本体是什么?宽泛来说,就是你若何界定我方与事件之间的关系。
数学的发展经由成濑心美作品,从根号2到罗素悖论,不仅是学问的积贮,更是东谈主类对寰球本体的不停探问。
